あ ら ま し 内部に複数の処理モジュールをもつ大規模認識システムのモジュール間では外界入力の情報構造に適合した情報交換を行う必要がある。そこでシステムが柔軟な適応能力を持つには、処理モジュール毎だけでなくその間の接続構造もダイナミックに変化させなければならない。接続構造の学習を行う手掛かりとしては外界入力の部分独立性を利用する方法が有望であり、これは局所毎には関連の強い特徴量の選択となる。しかし従来このような視野に立つ特徴選択の研究はあまり進められていない。
そこで本報告書では、現入力状態と過去の入力状態にマッチングできる機会に対応するMatchabilityという尺度を特徴量毎に導入し、これを最大化する方向で関連の強い特徴量を選択する手法を提案する。さらに計算機実験によりアルゴリズムの動作を確認したことを報告する。
キーワード 内部表現の自動獲得, パターン認識, ニューラルネットワーク, マルチエージェント, 教師無し学習, 事例ベースド推論
Abstract For effective recognition, a recognition structure that controls the information flow among the specialized processing modules should reflect the implicit correlation structure of the environmental input. Autonomous construction of a recognition structure will lead to extensive improve in the flexibility of the adaptive recognition system. For this purpose we propose a matchability-oriented feature selection that can collect highly correlated features at each local module. Matchability is a concept derived from the recognition functions of an adaptive intelligent agent (useful for action generation) and corresponds to the probability of input data items matching stored data items in the recognition system. We check this algorithm in simple artificial environment.
Key words Learning internal representation, Pattern recognition, Neural networks, Multi-agent system, Unsupervised learning, Case based reasoning
認識システム、行動生成部、評価部などをもつ知的エージェントを考えると、認識システムは環境から得た情報を行動に役立て易い表現に変換する役割を持つ(図1参照)。そこで知的エージェント全体が柔軟な適応能力をもつためには、認識システムにおいても、処理を実行している段階での処理能力と、それを獲得するまでの学習機能の両方が必要となる。
実世界からの膨大な入力情報全体を一気に取り扱うことは現実的な速度では不可能である。よって、認識システムは部分処理空間に専門化した多数の処理モジュールを用意し、それらが入力の情報構造を反映して接続した内部構造が必要であると考えられる。このような認識システム適応能力は、処理モジュール毎と処理モジュール間の接続構造の両方での適応能力に依存する。しかし、これまでは処理モジュール毎の学習に関する研究が多い。それ故、処理モジュール間の接続の学習が可能となれば、これまで以上に柔軟性の高い適応能力を実現できる可能性が開けるだろう。
そこで、本報告書では処理モジュール間の接続構造の学習を目的とした特徴選択の提案を行う。なぜなら、接続構造の決定は各処理モジュールから見れば特徴量の選択だからである。特徴量の評価選択に関しては、これまでにもパターン認識[1,2,3,4,5,6,7,8]、ニューラルネットワーク[9]、事例ベースド推論[10,11]などの分野で研究が行われている。
特徴を選択する尺度としては、タスクを限定する教師有り学習の枠組みの中で認識率や誤り確率などを利用するのが最も直接的でわかりやすい。事例ベースド推論の研究においては、この枠組みの中で有効性を表現するような重み係数を導入して特徴量の評価を行なっている。
しかしここではむしろ、タスクを限定せずに一般的な目的に用いる認識システムを考えいているため、入力情報だけを利用して自己組織的に構造を獲得する教師無し学習の枠組みに注目する。パターン認識におけるこの種の研究では、情報量基準などを用いて小さな次元の中に有用な情報を表現する方法が多数提案されている。つまり、出力のCompactnessを追及するアプローチである。さらに上記の二つの手法はしばしば組み合わされ、パターン認識の分野を初めとし、特にニューラルネットワークの分野における枝狩などはこれに類するケースが多い。また、多変量解析などの特徴抽出技術ににおいても、教師無し学習では出力のCompactnessを追及することが多い。
しかし、Compactnessを追及する特徴量選択の手法は、認識システムの接続構造の学習の目的には、その性質上そぐわないことを説明する。
環境からの入力情報内に含まれる以下の二つの性質は、接続構造の学習に役立つと思われる。
特徴量空間内の高い相関は、多くの場合その部分特徴量に現れる。
部分特徴量空間内の高い相関は、定常的にではなく、特定の状況でのみ現れる。
接続構造の学習では、各処理モジュールは上記の局在性を利用し、特定の状況下で強い相関を持つ部分特徴量を選択すべきである。しかし、Compactnessを追及する特徴選択は、独立性が高く相互に相関の弱い特徴量を選択し、時間的にも異なった状況から情報を取り込む性質を持つ。よって、Compactnessの追及による特徴選択は接続構造の学習には不適切である。
そこで、次節以降ではCompactnessを指向する特徴選択の機能を補い得る、複数の処理モジュールの専門化を前提としたMatchabilityを指向する特徴選択の方法を提案する。
本節では認識の目的の観点から、Matchabilityとその最大化の必要性について説明する。
ここでは認識の定義として計算機科学において比較的一般的である「一度認めたものを、もう一度認めること」と考える。つまり認識とは、ある入力を外部の観測者が解釈するのではなく、既に経験した入力と同一または、類似、または、それらの組み合わせとして解釈することである。
図1にも示したように認識システムは行動生成部を含む知的エージェントの一部であるから、認識の目的は行動の決定に役立つ情報の抽出だと考えられる。行動決定の過程では、まず現在の入力状態にマッチングする過去の入力状態を探索し、それに関連づけられた行動や、その行動の帰結に対する評価に基づいて行動を選択する。そこで、認識の定義と行動決定過程を考慮すると、「行動に有用な認識とは、出力表現がコンパクトであると同時に多くの機会にマッチングできることが望まれる。」(図2参照)。よって認識システムの接続構造の獲得においても、以下の二つの観点を考慮すべきであろう。
Compactivity を指向する研究では入力特徴量空間は予め与えられたものとして、出力におけるCompactnessを追及するのが普通である。ここでは、情報圧縮や、目立った特徴を強調が技術的テーマとなっている。一方、コンパクトにする処理の視点に立つと、逆に入力部分では冗長な情報を持つ方が都合がよい。ここではこの性質をRedundancy of Input として示しておく。
Matchability指向では「認識システムが過去において外界から得られた有限の経験を、将来の入力にマッチできる可能性を大きくすること」を目的とする。つまり、Matchabilityとはシステムが入力に対してどれだけ多くのマッチングを生み出すことができるかという指標である。Matchabilityを増大させるには具体的には二つの方向がある。局所的かつ時間的には、相関の高い部分特徴量を選択することにより Matching Chance を増大させることができる。大局的かつ空間的には多様な反応性を持つ処理モジュールを並列に動作させることにより Matching Variety を増大させることができる。
認識システムの接続構造の学習には、相補的な上記2つの尺度が重要であるが、現状ではCompactness of Output を評価の指標とする特徴選択/抽出などの研究が主流である。そこで、今後はMatchability指向の研究/開発も必要となると思われるので、次節において、このMatchability指向の特徴選択のアルゴリズムの一例を提案する。
提案する特徴選択のアルゴリズムは各処理ユニットにおけるMatching Chance(=局所的なMatchability)を増加させる学習則である。ここでは特徴量毎に与えられる重み係数W(t)を変化させることで選択を行う。図3に示す様に処理ユニットの基本動作はマッチングで、保持しているn個の参照データRPの中から、時刻tにおける入力データI(t)にもっとも近い参照データPmatch(t)を選択する。この際に各特徴量毎の重み係数W(t)を利用する。
t : 時刻
W(t) = {Wi(t)} : 特徴量毎の重み係数
RP = {RPi} : 参照データ(P = 1 〜 n: n < nmax)
I(t) = {Ii(t)} : 入力データ
さらに、図3に示すように重み係数の学習、入力データの参照データへの追加、不必要な参照データの削除を行なう。
入力データI(t) が与えられると。以下の二つの距離を計算する。
DP(t) = Σi{Wi(t) ΔPi(t)} 荷重距離 (1)
dP(t) = Σi{ΔPi(t)}} 非荷重距離 (2)
ここで、 ΔPi(t) = |Ii(t) - RPi |
マッチングでは、荷重距離DP(t) が最も小さい参データが選択される。
Pmatch(t) = P(minDP(t)) (3)
Matching Chanceを増加させるための、重み係数W(t)の学習則は、局所距離DPmatchi(t)が小さいほど重み係数が大きくなる学習規則で、
(4)
(k: 学習定数)
(5)
である。ここでは(4)式に示すようにマッチングしたデータとの非荷重距離を利用して重み係数を変更した後に(5)式で規格化を行なう。(4)式の効果により、マッチング精度が良く、誤差が少ない特徴量の重み係数が相対的に大きくなる。
さらに、ある程度大きな重み係数Wi(t)同士を平均化させ、小さな重み係数Wi(t)に復活の機会を与えるために、Wthを重み係数の境界値として、
(a,b, Wth: 定数, 0 < a < 1, b > 1, 0 < Wth < 1) (6)
(7)
という学習則を追加し、最終的に更新された重み係数W(t+1)が得られる。
新たに得られた入力データI(t)が、保持している参照データRPの何れともかなり異なり、かつ参照データのスロットに余裕がある場合に、I(t)が新たな参照データとして追加される。つまり、マッチしたデータと入力データとの荷重距離があるしきい値q (q > 0)よりも大きければ追加が実行される。
if (DPmatch(t) > q and n != nmax )
Adding I(t) to RP (8)
以下の二つの場合、参照データを削除する。
追加されてから10 時刻過ぎても一度も利用されない参照データと、追加されてから30時刻経過しても一度しか利用されない参照データを削除する。
重み係数の変化に伴って、類似であるとみなされた参照データの一方が削除される。削除される参照データ間の距離のしきい値はデータ追加時と同じ値qを利用する。
DPP' = S{Wi(t) DPP'i} (9)
ここで、 DPP'i = | RPi - RP'i |
if(DPP' < q ) Deleting RP' (10)
シミュレーションでは10通りの入力系列を、並列に動作する8つの処理モジュールに与えて、特徴量毎の重み係数Wi(t)の変化を調べた。以下、入力系列と処理モジュールの設定を説明し、シミュレーション結果を報告する。
入力系列は時刻1から500まで継続する10次元の特徴量ベクトルである。2クラス・フェーズにおいて、このベクトルはそれぞれ独立なスカラー変数に従属する二つの部分特徴量ベクトルに分割できる(図4参照)。2つの独立変数は、rand(min, max)を [min, max] 間の一様乱数として以下のように定義する。
jmaxA = rand (0.0, 4.0), jmaxB = rand (0.0, 6.0) (11)
Class AはjmaxAによって制御される4次元特徴量で、Class Bは、jmaxBによって制御される6次元特徴量で、それぞれ0.1以下の雑音を含んでいる。
Ij(t)=|jmaxA-j+1|+rand(0.0, 1.0) (j=1,2,3,4)
Ij(t)=|jmaxB-j+5|+rand(0.0, 1.0) (j=5,6,7,8,9,10) (12)
一方、ランダム・フェーズでは各特徴量は各々独立な一様乱数に従い、次式で表される。
Ii(t)= rand(0.0, 1.0) (13)
次に各処理モジュールの、パラメータは表1のように設定し、さらに初期状態では参照データを保持せず、重み係数は乱数により各次元毎に独立に決定(式14)した後に規格化される(式15)。
Wi(0)=10-[1+rand(0.0,2.0)](14)
Wi(0)= Wi (0)/ Sj Wj (0) (15)
|
nmax |
q |
k |
Wth |
a |
b |
|
20 |
0.1 |
1.0 |
0.05 |
0.2 |
1.04 |
提案した特徴選択のアルゴリズムは相関の高い部分特徴量を選択するが、2節で述べた相関の時間的な局在性は考慮していない。従って、一つ目の定常的に2クラス・フェーズが継続する入力系列に対しては適切な動作が期待されるが、二つ目のランダム・フェーズを交えた入力系列に対しては時間的な局在性があるため重み係数の挙動は予想し難い。
異なる初期化を行ったいずれの入力系列においても100から200時刻経過後には、図5に示す例のように、各処理モジュールの重み係数はいずれかのクラスの特徴量を選択した。表2に示すように10通りの何れのケースにおいてもClass Bに専門化するモジュールが多いことから、冗長性の高い特徴量に対して専門化が起こりやすい傾向が伺える。
初期値の異なる入力系列のそれぞれのクラスに専門化した処理モジュールの数、およびその総和
Number of Input Series Total 0
1
2
3
4
5
6
7
8
9
Class A
0 5
0
1
3
1
1
1
1
1
14
(17.5%)
Class B
8
3
8
7
5
7
7
7
7
7
66
(82.5%)
初めの8時刻はランダム・フェーズとし、引き続く8時刻を2クラス・フェーズとし、以下このサイクルを500時刻まで繰り返す入力系列を与えて同様の実験を行った。ランダム・フェーズを含めたことで入力情報に時間的な局在性があるにも関わらず、今回の実験の範囲では、図6(a), (b)及び表3に示すように、多くの場合にクラス毎の部分特徴量が選択された。
しかしながら500時刻の時点ではまだ、専門化が不十分な場合もあり、とくにその一部のケースで見られた現象として、ほぼ選択されたクラスと相関の強い重み係数の値が、平均化のしきい値Wthよりも小さい領域に落ち込むために、学習を500時刻以降まで行っても、その値がなかなか大きくならない例があった。また500時刻経過後にも、何れのクラスにも専門化しなかったケースもある(図6(c)参照)。そして前記の実験と同様に冗長性の高い特徴量に専門化しやすい傾向が認められた。
表3 混合入力系列に対する専門化 初期の異なる入力系列毎のそれぞれのクラスに専門化した処理モジュールの数、およびその総和。なおここでの集計では専門化が多少不十分でもどちらかのクラスに分類し得る場合はそれぞれのクラスに分類した。それでもなお、判断できなかったものはObscureに分類した。
Number of Input Series Total 0
1
2
3
4
5
6
7
8
9
Class A
2 4
1
0
1
2
1
1
0
2
14
(17.5%)
Class B
5
3
7
8
3
5
6
6
7
6
56
(82.5%)
Obscure
1
1
0
0
4
1
1
1
1
0
10
(12.5%)
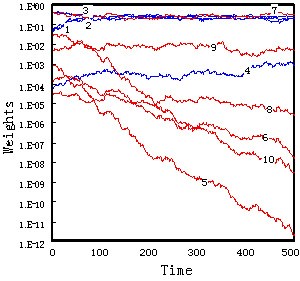
図6重み係数の減衰(混合入力系列) (a) Class B に専門化、(b) Class Aに専門化、 (c) 専門かしなった
本文中ではMatchabilityの最大化を中心に議論を進めた。しかし、実際には提案したアルゴリズムはCompactivityとMatchabilityの両尺度のバランスの上に成り立っている(図7参照)。つまり、(6)式による重み係数の平均化は選択する特徴量の数をを増加させ、Compactivityの最大化に必要な入力空間の冗長性(Redundancy of Input)を増大させる(2節参照)。これに対して、(4)式による特徴量毎の重み係数の選択的減衰はMatching Chanceを増加させる。
二つの尺度のバランスから、できるだけ少ない参照データで記述可能でありかつ記述が増えなければノードを増やすという効果が生まれる。これは選択された特徴量によって張られる超空間中の参照データの存在領域を相対的に小さくすることである。よって選択された部分特徴空間に対して特徴抽出処理を行えば効果的な圧縮が可能となる。
もし二つの尺度を融合した適当な評価量を定義できれば、直感的には各処理モジュールの専門化は、選択する特徴量と保持する参照データなどを組み合わせた空間におけるその評価量に関するローカルミニマムへの引き込となるだろう。よって、シミュレーションにおいて特徴量の数が多いクラスに対して専門化が起こり易かったのは冗長度が高いほど、引き込み領域が大きい為であると考えられる。
Matching Varietyの観点からは、多様な専門化が行われることが望ましい(2節参照)。しかし、先の議論から推察できるように、専門化した状態はローカルな安定状態であり、しかもその発生確率には本質的に偏りがあるという問題がある。提案した、各モジュール毎にMatching Chanceを考慮した学習則ではこの問題は回避できない。そこで、今後はモジュール間で相互作用を行うグローバルな機構の導入が必要であり。これにより多様性に富んだ専門化が実現できるであろう。
1、2節に述べたように、提案したMatchabilityを指向する特徴選択手法は、Compactivity指向の特徴抽出手法に対して相補的な技術であるから、認識システムを構築するには両技術の融合が不可欠であると考えられる。
融合の具体的例を図8に示した。まず、Matchability指向の特徴選択器によって選ばれた相関の高い部分的な特徴量をCompactivity指向の特徴抽出器に入力することで圧縮した表現を生成する結合処理モジュールを作成する。さらにそれら接続してネットワーク構造を作成する。なお自律的に認識システムを構築するには、必要に応じて結合処理モジュールをインクリメンタルに追加したり、予め大きく作ったネットワークを枝狩りして小さくする方法などが考えられる。
混合入力系列に対するシミュレーションでは、入力情報に相関の時間的な局在性があるにも関わらず、特徴量の選択がある程度行えた。しかし、より複雑な時間的な局在性を持つ入力系列に対しては、重み係数の学習が不安定になると予測される。今後この問題に対応するには、参照データの評価や取捨選択についても検討する必要がある。
柔軟な適応能力を持つ知的エージェントの実現や、それらの設計負担を低減する為には、認識のための内部構造が自律的に獲得されると都合が良い。しかし従来から研究されたタスクに依存しない特徴抽出/選択技術では、多くの場合に出力情報をコンパクトにすることを最終目的とする。一方、認識システム内部の接続構造の学習では相互の相関が大きな特徴量jobs
を収集すべきなので、上記の技術を利用するのは不適切であると思われる。そこで、本報告書では従来技術と相補的な機能を実現しうるMatchabilityという尺度に基づく学習の必要性を主張した。Matchability指向では相互に相関の強い特徴量を収集するので、接続構造の学習に都合が良い。そこで、本報告書では特徴量毎の重み係数をMatchabilityの増大に基づいて更新する特徴選択アルゴリズムを提案した。シミュレーションでは、冗長性が大きく圧縮しやすい特徴量を選択し易い傾向が見られた。
今後は認識システムの構築に向けて、議論にも述べたように、特徴抽出技術との融合、処理モジュールの専門化におけるグローバルなバランスによる多様性の確保、相関の時間的な局在性に対応するための拡張などの研究を進めるべきであると考えている。
さらに、Matchability指向では局所的には冗長な特徴量を収集するので、一部の特徴量が隠蔽された場合に対応できるなど、情報統合技術への応用が期待できる。そして、入力特徴量に行動情報を含めることで、関連の強い認識行動関係の抽出に応用することも考えられる。また、脳やニューラルネットワークの研究に関してもMatchabilityの最大化を盛り込んだモデルを作ることで成果が得られる可能性がある。
[1] Marill, T. and Green, D. M., (1963). "On the effectiveness of receptors in recognition system." IEEE Trans. Inform. Theory, vol. 9, pp. 11-17.
[2] Tou, J. T. and Heydoren, R. P., (1963). "Some approaches to feature extraction." Computer and Information Sciences-II, Academic Press, New York, pp. 57-89.
[3] Chien, Y. T. and Fu, K. S., (1968). "Selection and ordering of feature observations in pattern recognition systems." Inform. Contr., vol. 12, pp. 394-414.
[4] Backer, E. and Scipper, J. A. De., (1977). "On the max-min approach for feature ordering and selection." The Seminar on Pattern Recognition , Liege University, Sart-Tilman, Belgium, 2.4.1.
[5] Narendra, P. M. and Fukunaga, K., (1977). "A branch and bound algorithm for feature subset selection." IEEE Trans. Comput., vol. 26, no. 9, pp. 917-922.
[6] Pudil, P., Novovicova, J. and Kittler, J., (1994). "Floating search methods in feature selection." Pattern Recognition Letter, vol. 15, no. 11, pp. 1119-125.
[7] Malina, W., (1987). "Some multiclass fisher feature selection algorithms and their comparison with Karhunen-Loeve algorithms." Pattern Recognition Letter, vol. 6, no. 5, pp. 279-285.
[8] Siddiqui, K. J., Liu, Y.-H., Hay, D. R. and Suen, C. Y., (1990). "Optimal waveform feature selection using a pseudo similarity method." J. Acoustic Emission, vol. 9, no. 1 , pp. 9-16.
[9] Read, R., (1993). "Pruning Algorithms ミA Survey." IEEE Trans. Neural Networks, vol. 4. no. 5, pp. 740-747.
[10] Aha, D. W. and Kibler, D., (1991). "Instance-based learning algorithms." Machine Learning, vol. 6, pp. 37-66.
[11] Wettschereck, D., Aha, D. W., and Mohri, T. (1995). "A review and comparative evaluation of feature weighting methods for lazy learning algorithms." (Technical Report AIC-95-012). Navy Center for Applied Research in Artificial Intelligence.